BN Boparan credit default no evidence

Bayesian net and Boparan 7.625% 30 Nov 2025 Prospectus

This blog is a follow-up on a first naive modelling of Matalan notes using Bayesian nets. Bayesian nets are a good tool to quantify qualitative knowledge, as explained here.

The work presented in this blog post was mostly realized by Zhiyuan Shen in the context of his financial mathematics master of science at HKUST.

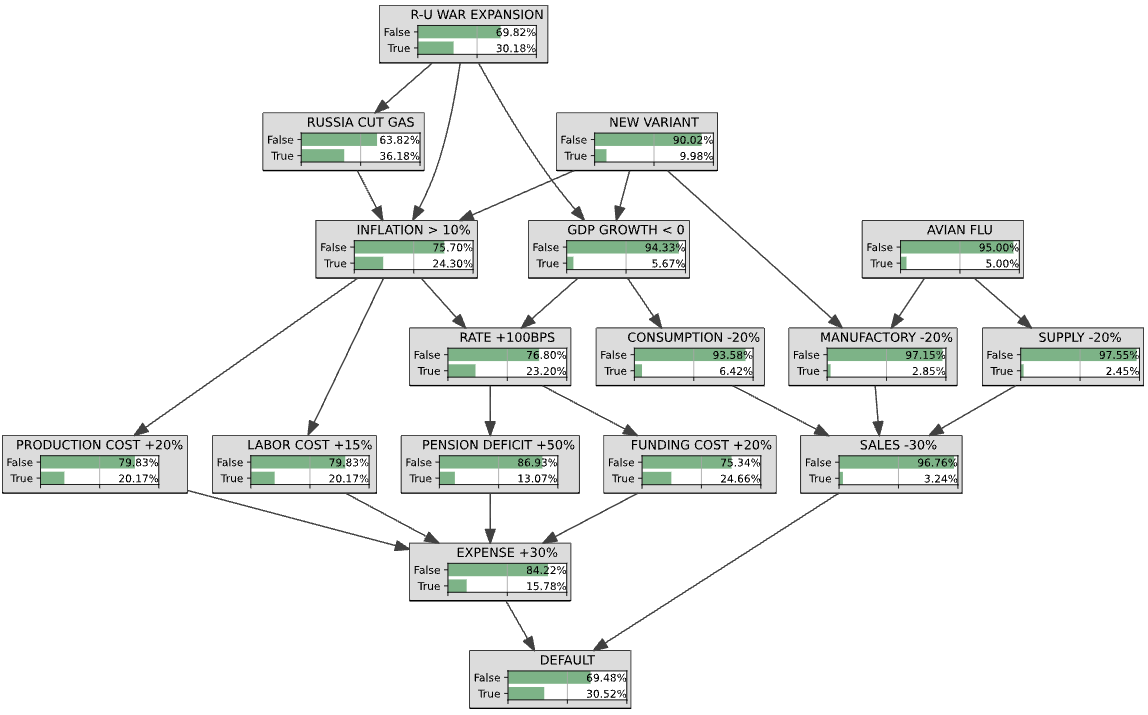
The purpose of this work is to build a Bayesian network which would summarise and articulate together the risks faced by 2 Sisters Food Group, a private company in the UK manufacturing food, founded in 1993 by Ranjit Singh Boparan.

The issuer of the 7.625% 30 Nov 2025 senior secured notes is a SPV (Boparan Finance plc), and the GBP 475 million debt is guaranteed by several companies in the Boparan Group.

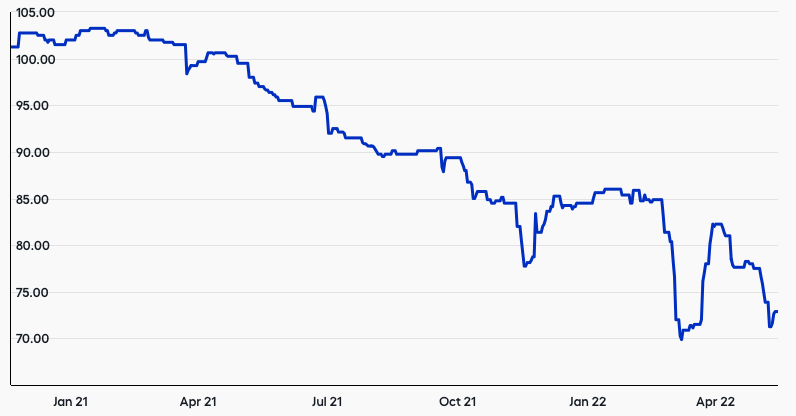
Bond price of Boparan 25

Source: WiseAlpha

Current YTM of these notes is about 18.4%.

A great deal of information can be learnt from the Notes Prospectus (500 pages).

As a side note: How can we structure and mine the prospectus information efficiently and systematically? I have been pondering this question for the past 5 years. As far as data vendors are concerned, they just act as aggregators (which is already helpful) but do not provide further added value. I have talked to a few of them: Some were in the early stages of starting a ‘data analytics’ effort, but without a clear roadmap and timeline, and asking clients to help them figure out what was important.

Zhiyuan went through the prospectus of the notes, and extracted some risk factors with potential material impact on the company. Those risk factors are important to track in real time. A fundamental analyst in a discretionary setup should keep them in mind at all times. For the quantitative systematic trader, good luck! This is yet another tricky data structuration challenge… which would require a higher level understanding of the news flow (think knowledge graph) than a naive +1, 0, -1 sentiment in order to reconciliate news information with extracted risk factors information. Once again, this is relatively easy to do so for a good discretionary analyst, but the cognitive load would be quite high to cover a large number of companies.

Besides monitoring companies one by one, these Bayesian nets could help factor some common risk factors (say inflation) while keeping some others specific (say avian flu).

Question: How can we efficiently merge the Matalan Bayesian net with the Boparan Bayesian net (presented in this blog)?

I suspect that the merge may yield to some inconsistencies (incompatible CPTs or invalid JPT). What if we would like to merge 100s more? 1000s more? Ultimately, we want to have a joint view on all the issuers (say UK HY).

import pyAgrum as gum
import pyAgrum.lib.notebook as gnb
import pyAgrum.lib.mn2graph as m2g


bn = gum.BayesNet('Boparan default probability')

variables = [
    'R-U WAR EXPANSION',
    'RUSSIA CUT GAS',
    'NEW VARIANT',
    'AVIAN FLU',
    'INFLATION > 10%',
    'GDP GROWTH < 0',
    'RATE +100BPS',
    'PENSION DEFICIT +50%',
    'FUNDING COST +20%',
    'PRODUCTION COST +20%',
    'LABOR COST +15%',
    'CONSUMPTION -20%',
    'MANUFACTORY -20%',
    'SUPPLY -20%',
    'EXPENSE +30%',
    'SALES -30%',
    'DEFAULT'
]


(r_u_war_expansion, russia_cut_gas, new_variant, avian_flu, high_inflation,
 low_gdp, rate_increase, pension_deficit_increase, funding_cost_increase,
 production_cost_increase, labor_cost_increase, consumption_decrease,
 manufactory_shut_down, supply_decrease, expense_increase, sales_decrease,
 default) = [
    bn.add(gum.LabelizedVariable(name, '', ['False', 'True']))
    for name in variables]

edges = [
     ('R-U WAR EXPANSION', 'INFLATION > 10%'),
     ('R-U WAR EXPANSION', 'GDP GROWTH < 0'),
     ('R-U WAR EXPANSION', 'RUSSIA CUT GAS'),
     ('RUSSIA CUT GAS', 'INFLATION > 10%'),
     ('NEW VARIANT', 'INFLATION > 10%'),
     ('NEW VARIANT', 'GDP GROWTH < 0'),
     ('NEW VARIANT', 'MANUFACTORY -20%'),
     ('AVIAN FLU', 'MANUFACTORY -20%'),
     ('AVIAN FLU', 'SUPPLY -20%'),
     ('INFLATION > 10%', 'RATE +100BPS'),
     ('RATE +100BPS', 'PENSION DEFICIT +50%'),
     ('RATE +100BPS', 'FUNDING COST +20%'),
     ('INFLATION > 10%', 'PRODUCTION COST +20%'),
     ('INFLATION > 10%', 'LABOR COST +15%'),
     ('GDP GROWTH < 0', 'CONSUMPTION -20%'),
     ('GDP GROWTH < 0', 'RATE +100BPS'),
     ('PENSION DEFICIT +50%', 'EXPENSE +30%'),
     ('FUNDING COST +20%', 'EXPENSE +30%'),
     ('PRODUCTION COST +20%', 'EXPENSE +30%'),
     ('LABOR COST +15%', 'EXPENSE +30%'),
     ('CONSUMPTION -20%', 'SALES -30%'),
     ('MANUFACTORY -20%', 'SALES -30%'),
     ('SUPPLY -20%', 'SALES -30%'),
     ('EXPENSE +30%', 'DEFAULT'),
     ('SALES -30%', 'DEFAULT'),
]

for edge in edges:
    bn.addArc(*edge)

bn

print(bn)

BN{nodes: 17, arcs: 25, domainSize: 131072, dim: 130}

bn.cpt('R-U WAR EXPANSION')[{}] = [0.7, 0.3]
bn.cpt('NEW VARIANT')[{}] = [0.9, 0.1]
bn.cpt('AVIAN FLU')[{}] = [0.95, 0.05]

bn.cpt('RUSSIA CUT GAS')[{'R-U WAR EXPANSION': 0}] = [0.7, 0.3]
bn.cpt('RUSSIA CUT GAS')[{'R-U WAR EXPANSION': 1}] = [0.5, 0.5]

bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 0,
                           'RUSSIA CUT GAS': 0,
                           'NEW VARIANT': 0}] = [0.9, 0.1]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 1,
                           'RUSSIA CUT GAS': 0,
                           'NEW VARIANT': 0}] = [0.7, 0.3]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 0,
                           'RUSSIA CUT GAS': 1,
                           'NEW VARIANT': 0}] = [0.7, 0.3]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 0,
                           'RUSSIA CUT GAS': 0,
                           'NEW VARIANT': 1}] = [0.98, 0.02]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 1,
                           'RUSSIA CUT GAS': 1,
                           'NEW VARIANT': 0}] = [0.4, 0.6]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 1,
                           'RUSSIA CUT GAS': 0,
                           'NEW VARIANT': 1}] = [0.8, 0.2]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 0,
                           'RUSSIA CUT GAS': 1,
                           'NEW VARIANT': 1}] = [0.8, 0.2]
bn.cpt('INFLATION > 10%')[{'R-U WAR EXPANSION': 1,
                           'RUSSIA CUT GAS': 1,
                           'NEW VARIANT': 1}] = [0.5, 0.5]

bn.cpt('GDP GROWTH < 0')[{'R-U WAR EXPANSION': 0,
                        'NEW VARIANT': 0}] = [0.99, 0.01]
bn.cpt('GDP GROWTH < 0')[{'R-U WAR EXPANSION': 0,
                        'NEW VARIANT': 1}] = [0.8, 0.2]
bn.cpt('GDP GROWTH < 0')[{'R-U WAR EXPANSION': 1,
                        'NEW VARIANT': 0}] = [0.9, 0.1]
bn.cpt('GDP GROWTH < 0')[{'R-U WAR EXPANSION': 1,
                        'NEW VARIANT': 1}] = [0.7, 0.3]

bn.cpt('RATE +100BPS')[{'INFLATION > 10%': 0,
                        'GDP GROWTH < 0': 0}] = [0.8, 0.2]
bn.cpt('RATE +100BPS')[{'INFLATION > 10%': 0,
                        'GDP GROWTH < 0': 1}] = [0.99, 0.01]
bn.cpt('RATE +100BPS')[{'INFLATION > 10%': 1,
                        'GDP GROWTH < 0': 0}] = [0.6, 0.4]
bn.cpt('RATE +100BPS')[{'INFLATION > 10%': 1,
                        'GDP GROWTH < 0': 1}] = [0.98, 0.02]

bn.cpt('PRODUCTION COST +20%')[{'INFLATION > 10%': 0}] = [0.9, 0.1]
bn.cpt('PRODUCTION COST +20%')[{'INFLATION > 10%': 1}] = [0.5, 0.5]

bn.cpt('LABOR COST +15%')[{'INFLATION > 10%': 0}] = [0.9, 0.1]
bn.cpt('LABOR COST +15%')[{'INFLATION > 10%': 1}] = [0.5, 0.5]

bn.cpt('PENSION DEFICIT +50%')[{'RATE +100BPS': 0}] = [0.95, 0.05]
bn.cpt('PENSION DEFICIT +50%')[{'RATE +100BPS': 1}] = [0.6, 0.4]

bn.cpt('FUNDING COST +20%')[{'RATE +100BPS': 0}] = [0.95, 0.05]
bn.cpt('FUNDING COST +20%')[{'RATE +100BPS': 1}] = [0.1, 0.9]

bn.cpt('CONSUMPTION -20%')[{'GDP GROWTH < 0': 0}] = [0.98, 0.02]
bn.cpt('CONSUMPTION -20%')[{'GDP GROWTH < 0': 1}] = [0.2, 0.8]

bn.cpt('MANUFACTORY -20%')[{'NEW VARIANT': 0,
                        'AVIAN FLU': 0}] = [0.99, 0.01]
bn.cpt('MANUFACTORY -20%')[{'NEW VARIANT': 0,
                        'AVIAN FLU': 1}] = [0.8, 0.2]
bn.cpt('MANUFACTORY -20%')[{'NEW VARIANT': 1,
                        'AVIAN FLU': 0}] = [0.9, 0.1]
bn.cpt('MANUFACTORY -20%')[{'NEW VARIANT': 1,
                        'AVIAN FLU': 1}] = [0.7, 0.3]

bn.cpt('SUPPLY -20%')[{'AVIAN FLU': 0}] = [0.99, 0.01]
bn.cpt('SUPPLY -20%')[{'AVIAN FLU': 1}] = [0.7, 0.3]

bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 0,
                        }] = [0.99, 0.01]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 0,
                        }] = [0.8, 0.2]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 0,
                        }] = [0.8, 0.2]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 0,
                        }] = [0.8, 0.2]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 1,
                        }] = [0.8, 0.2]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 0,
                        }] = [0.8, 0.4]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 0,
                        }] = [0.6, 0.4]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 1,
                        }] = [0.6, 0.4]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 0,
                        }] = [0.6, 0.4]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 1,
                        }] = [0.6, 0.4]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 1,
                        }] = [0.6, 0.4]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 0,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 1,
                        }] = [0.4, 0.6]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 0,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 1,
                        }] = [0.4, 0.6]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 0,
                        'FUNDING COST +20%': 1,
                        }] = [0.4, 0.6]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 0,
                        }] = [0.4, 0.6]
bn.cpt('EXPENSE +30%')[{'PRODUCTION COST +20%': 1,
                        'LABOR COST +15%': 1,
                        'PENSION DEFICIT +50%': 1,
                        'FUNDING COST +20%': 1,
                        }] = [0.2, 0.8]

bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 0,
                      'MANUFACTORY -20%': 0,
                      'SUPPLY -20%': 0,
                      }] = [0.99, 0.01]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 1,
                      'MANUFACTORY -20%': 0,
                      'SUPPLY -20%': 0,
                      }] = [0.8, 0.2]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 0,
                      'MANUFACTORY -20%': 1,
                      'SUPPLY -20%': 0,
                      }] = [0.8, 0.2]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 0,
                      'MANUFACTORY -20%': 0,
                      'SUPPLY -20%': 1,
                      }] = [0.8, 0.2]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 1,
                      'MANUFACTORY -20%': 1,
                      'SUPPLY -20%': 0,
                      }] = [0.6, 0.4]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 1,
                      'MANUFACTORY -20%': 0,
                      'SUPPLY -20%': 1,
                      }] = [0.6, 0.4]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 0,
                      'MANUFACTORY -20%': 1,
                      'SUPPLY -20%': 1,
                      }] = [0.6, 0.4]
bn.cpt('SALES -30%')[{'CONSUMPTION -20%': 1,
                      'MANUFACTORY -20%': 1,
                      'SUPPLY -20%': 1,
                      }] = [0.4, 0.6]

bn.cpt('DEFAULT')[{'EXPENSE +30%': 0,
                   'SALES -30%': 0,
                   }] = [0.75, 0.25]
bn.cpt('DEFAULT')[{'EXPENSE +30%': 1,
                   'SALES -30%': 0,
                   }] = [0.5, 0.5]
bn.cpt('DEFAULT')[{'EXPENSE +30%': 0,
                   'SALES -30%': 1,
                   }] = [0.25, 0.75]
bn.cpt('DEFAULT')[{'EXPENSE +30%': 1,
                   'SALES -30%': 1,
                   }] = [0.1, 0.9]

gnb.sideBySide(
    bn.cpt('R-U WAR EXPANSION'),
    bn.cpt('NEW VARIANT'),
    bn.cpt('AVIAN FLU'),
)
gnb.sideBySide(
    bn.cpt('INFLATION > 10%'),
    bn.cpt('RUSSIA CUT GAS'),
)
gnb.sideBySide(
    bn.cpt('GDP GROWTH < 0'),
    bn.cpt('RATE +100BPS'),
)
gnb.sideBySide(
    bn.cpt('PENSION DEFICIT +50%'),
    bn.cpt('FUNDING COST +20%'),
)
gnb.sideBySide(
    bn.cpt('PRODUCTION COST +20%'),
    bn.cpt('LABOR COST +15%'),
)
gnb.sideBySide(
    bn.cpt('CONSUMPTION -20%'),
    bn.cpt('MANUFACTORY -20%'),
    bn.cpt('SUPPLY -20%'),
)
gnb.sideBySide(
    bn.cpt('EXPENSE +30%'),
    bn.cpt('SALES -30%'),
)
gnb.sideBySide(
    bn.cpt('DEFAULT'),
)

R-U WAR EXPANSION
False	True
0.7000	0.3000

NEW VARIANT
False	True
0.9000	0.1000

AVIAN FLU
False	True
0.9500	0.0500

			INFLATION > 10%
NEW VARIANT	RUSSIA CUT GAS	R-U WAR EXPANSION	False	True
False	False	False	0.9000	0.1000
	False	True	0.7000	0.3000
	True	False	0.7000	0.3000
	True	True	0.4000	0.6000
True	False	False	0.9800	0.0200
	False	True	0.8000	0.2000
	True	False	0.8000	0.2000
	True	True	0.5000	0.5000

	RUSSIA CUT GAS
R-U WAR EXPANSION	False	True
False	0.7000	0.3000
True	0.5000	0.5000

		GDP GROWTH < 0
NEW VARIANT	R-U WAR EXPANSION	False	True
False	False	0.9900	0.0100
False	True	0.9000	0.1000
True	False	0.8000	0.2000
True	True	0.7000	0.3000

		RATE +100BPS
GDP GROWTH < 0	INFLATION > 10%	False	True
False	False	0.8000	0.2000
False	True	0.6000	0.4000
True	False	0.9900	0.0100
True	True	0.9800	0.0200

	PENSION DEFICIT +50%
RATE +100BPS	False	True
False	0.9500	0.0500
True	0.6000	0.4000

	FUNDING COST +20%
RATE +100BPS	False	True
False	0.9500	0.0500
True	0.1000	0.9000

	PRODUCTION COST +20%
INFLATION > 10%	False	True
False	0.9000	0.1000
True	0.5000	0.5000

	LABOR COST +15%
INFLATION > 10%	False	True
False	0.9000	0.1000
True	0.5000	0.5000

	CONSUMPTION -20%
GDP GROWTH < 0	False	True
False	0.9800	0.0200
True	0.2000	0.8000

		MANUFACTORY -20%
AVIAN FLU	NEW VARIANT	False	True
False	False	0.9900	0.0100
False	True	0.9000	0.1000
True	False	0.8000	0.2000
True	True	0.7000	0.3000

	SUPPLY -20%
AVIAN FLU	False	True
False	0.9900	0.0100
True	0.7000	0.3000

				EXPENSE +30%
LABOR COST +15%	PRODUCTION COST +20%	FUNDING COST +20%	PENSION DEFICIT +50%	False	True
False	False	False	False	0.9900	0.0100
		False	True	0.8000	0.2000
		True	False	0.8000	0.2000
		True	True	0.6000	0.4000
	True	False	False	0.8000	0.2000
		False	True	0.6000	0.4000
		True	False	0.6000	0.4000
		True	True	0.4000	0.6000
True	False	False	False	0.8000	0.2000
		False	True	0.6000	0.4000
		True	False	0.6000	0.4000
		True	True	0.4000	0.6000
	True	False	False	0.8000	0.4000
		False	True	0.4000	0.6000
		True	False	0.4000	0.6000
		True	True	0.2000	0.8000

			SALES -30%
SUPPLY -20%	MANUFACTORY -20%	CONSUMPTION -20%	False	True
False	False	False	0.9900	0.0100
	False	True	0.8000	0.2000
	True	False	0.8000	0.2000
	True	True	0.6000	0.4000
True	False	False	0.8000	0.2000
	False	True	0.6000	0.4000
	True	False	0.6000	0.4000
	True	True	0.4000	0.6000

		DEFAULT
SALES -30%	EXPENSE +30%	False	True
False	False	0.7500	0.2500
False	True	0.5000	0.5000
True	False	0.2500	0.7500
True	True	0.1000	0.9000

ie = gum.LazyPropagation(bn)
ie.makeInference()

gnb.showInference(bn, evs={})

BN Boparan credit default no evidence

gnb.showInference(bn, evs={'LABOR COST +15%': 1})

BN Boparan credit default labor cost +15%

gnb.showInference(bn, evs={'AVIAN FLU': 1, 'LABOR COST +15%': 1})

BN Boparan credit default avian flu and labor cost +15%

gnb.showInference(bn, evs={'SALES -30%': 1, 'LABOR COST +15%': 1})

BN Boparan credit default sales -30% and labor cost +15%

Conclusion: I would not use this BN for any real trading, but it illustrates nicely the challenges one faces when building such models.

It would be interesting to add a few other UK food manufacturing companies as they may have many risk factors in common, as well as some of Boparan’s major customers such as Marks & Spencer or Asda which have sizeable debt trading.