How to sample uniformly over the space of correlation matrices? The onion method
How to sample uniformly over the space of correlation matrices? The onion method
The onion method is a method that samples exactly from the uniform distribution over the set of correlation matrices, a subset of $R^{\frac{d(d-1)}{2}}$.
The method is described in Behaviour of the NORTA Method for Correlated Random Vector Generation as the Dimension Increases (Section 4).
Basically, it starts with a one-dimensional matrix and grows it iteratively by adding extra rows chosen from an appropriate distribution.
This sampling procedure can be interesting when studying how some portfolio construction algorithms behave in- and out-sample, and how do they compare each other.
Onion method
import numpy as np
from numpy.random import beta
from numpy.random import randn
from scipy.linalg import sqrtm
from numpy.random import seed
seed(42)
def sample_unif_correlmat(dimension):
d = dimension + 1
prev_corr = np.matrix(np.ones(1))
for k in range(2, d):
# sample y = r^2 from a beta distribution
# with alpha_1 = (k-1)/2 and alpha_2 = (d-k)/2
y = beta((k - 1) / 2, (d - k) / 2)
r = np.sqrt(y)
# sample a unit vector theta uniformly
# from the unit ball surface B^(k-1)
v = randn(k-1)
theta = v / np.linalg.norm(v)
# set w = r theta
w = np.dot(r, theta)
# set q = prev_corr**(1/2) w
q = np.dot(sqrtm(prev_corr), w)
next_corr = np.zeros((k, k))
next_corr[:(k-1), :(k-1)] = prev_corr
next_corr[k-1, k-1] = 1
next_corr[k-1, :(k-1)] = q
next_corr[:(k-1), k-1] = q
prev_corr = next_corr
return next_corr
sample_unif_correlmat(3)
array([[ 1. , 0.36739638, 0.1083456 ],
[ 0.36739638, 1. , -0.05167306],
[ 0.1083456 , -0.05167306, 1. ]])
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
n = 1000
correlmats = [sample_unif_correlmat(3) for i in range(n)]
xs = [correlmat[0,1] for correlmat in correlmats]
ys = [correlmat[0,2] for correlmat in correlmats]
zs = [correlmat[1,2] for correlmat in correlmats]
for c, m, zlow, zhigh in [('r', 'o', -50, -25), ('b', 'o', -30, -5)]:
ax.scatter(xs, ys, zs, c=c, marker=m)
ax.set_xlabel('$\\rho_{12}$')
ax.set_ylabel('$\\rho_{13}$')
ax.set_zlabel('$\\rho_{23}$')
plt.show()
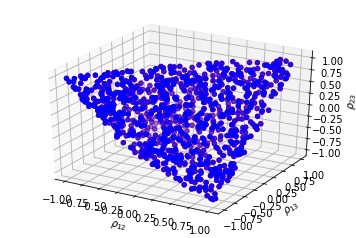
We can observe the shape of an elliptope, the set of all correlation matrices. We have effectively sampled uniformly from this set!